Probability distribution sampling in C# using StatDist and Troschuetz.Random

Introduction

Let’s talk about sampling probability density functions.

For example, imagine that you’re generating a combat encounter.⁰ You need to spawn several enemies, but not a fixed count - let’s assume a range of [1 .. 10] opponents.

At this point we could roll a d10 and call it a day, but that wouldn’t feel very creative. What if we’d prefer to usually choose a small number of opponents, and only occasionally challenge the player with a larger fight?

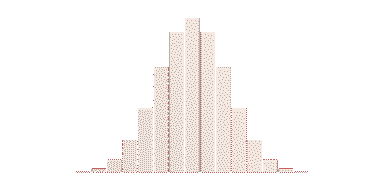
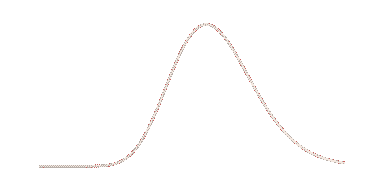
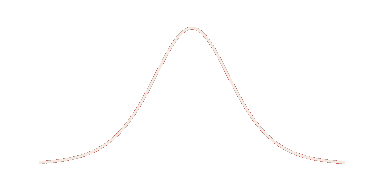
Basically, we want to sample a probability distribution that looks like this:

Binomial distribution with n = 30, p = 0.11 - usually yields a number around 3, but sometimes even up to 10.

Different scenario. You’re spawning some loot and need to decide whether to include a rare item. Again, if your game is simple a dice roll might be sufficient. But let’s assume that you wish the player to have a Luck stat that affects the drop chance nonlinearly. Consider these constraints:

• At low levels, you want the player to immediately feel the benefits of increasing their Luck
• Obviously, the drop probability cannot exceed 100%
• But at the same time it would be nice if stacking huge amounts of Luck still benefited the player somewhat, even if by a small amount

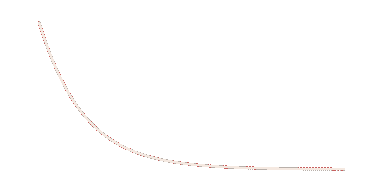
What we need is a random event that depends on a difficulty level with diminishing returns. Basically, we’re looking for a distribution with a cumulative distribution that looks something like this:

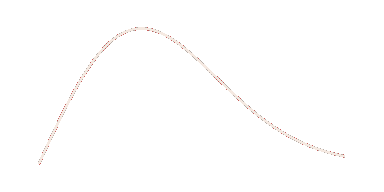
Cumulative distribution function for the Erlang distribution with k = 1, λ = 0.01.
In our example, 𝑥 represents our character’s Luck.
P(𝒳 < 𝑥) - the green area - represents the probability that Luck is sufficient to spawn the item.

These are just two examples, but what you probably want is some different probability distribution, with a set of parameters that is specific to your game or program.

If you’re a visual thinker, you might have a rough idea of what shape your imaginary reward value distribution is, but no idea how to represent it in code. How do we solve this? Here’s one workflow I like…

• Finding your dream distribution w/ StatDist
• Sampling distributions w/ Troschuetz.Random
• Generating random events w/ Troschuetz.Random
• Distributions supported by both Troschuetz.Random and StatDist
  • double Beta(double alpha, double beta);
  • int Binomial(double alpha /* trials */, int beta /* probability */);
  • double Cauchy(double alpha /* location */, double gamma /* scale */);
  • double ChiSquare(int alpha /* degrees of freedom */);
  • double ContinuousUniform(double alpha /* min */, double beta /* max */);
  • int DiscreteUniform(int alpha /* min */, int beta /* min */);
  • double Erlang(int alpha /* shape */, double lambda /* rate */);
  • double Exponential(double lambda /* rate */);
  • double FisherSnedecor(int alpha, int beta);
  • double Gamma(double alpha /* shape */, double beta /* scale */);
  • double Laplace(double alpha /* location */, double mu /* scale */);
  • double Logistic(double mu /* mean */, double sigma /* scale */);
  • double Lognormal(double mu /* mean */, double sigma /* standard deviation */);
  • double Normal(double mu /* mean */, double sigma /* standard deviation */);
  • double Pareto(double alpha /* scale */, double beta /* shape */);
  • int Poisson(double lambda /* rate */);
  • double Rayleigh(double sigma /* scale */);
  • double StudentsT(int nu /* degrees of freedom */);
  • double Triangular(double alpha /* min */, double beta /* mode */, double gamma /* max */);
  • double Weibull(double alpha /* shape */, double lambda /* scale */);

Finding your dream distribution w/ StatDist

StatDist is a cool little website that lets you plot dozens of common statistical distributions.

Distributions shown in red are not supported by Troschuetz.Random

Simply choose a distribution, input the parameters and you’ll get an overview of what the distribution is like. Thankfully, the scary equations are hidden by default, but there’s a Details button for the brave.

The graphs and the 𝑥 parameter (which lets us preview the value of the function at 𝑥) can be used to build intuition for how the distribution behaves by simply playing with it.

Sampling distributions w/ Troschuetz.Random

Troschuetz.Random is a library which implements various random number generators and distributions. In most cases, you can simply copy the parameters chosen using StatDist into the function call. Super convenient.

0
1
2
3
4
5
6
var random = new Troschuetz.Random.TRandom();

// get a random value based on some chosen distribution
double sample = random.Binomial(alpha: 30, beta: 0.1);

// clamp the value to our indended value range (recommended)
sample = Math.Clamp(sample, min: 0, max: 10);

This yields us a random 𝑥 based on the distribution we previously nailed down. No longer are we bound to the uniformly-distributed random numbers generated by System.Random - now we can sample any random distribution we like!

Generating random events w/ Troschuetz.Random

Sometimes we want to decide whether a random event has occured based on a parameter that represents difficulty.¹

If you ever used the System.Random class like this: random.Next() < 0.9 // 90% probability, then this is basically the same thing, except with TRandom we can use a more interesting, non-uniform distribution of random values. This allows us to have a non-linear relationship between the difficulty and the probability of the random event.²

Basically, you just do this:

0
1
2
3
4
5
6
7
8
9
10
11
var random = new Troschuetz.Random.TRandom();

// the "luck" value that we want our random value to undershoot
// (if you prefer to think in terms of a "difficulty" value instead, simply invert the final result)
double luck = 100;

// get a random value based on some chosen distribution
double sample = random.Erlang(alpha: 1, lambda: 0.01);

// test whether the random value is less than the player's "luck"
// (or higher than the "difficulty" value)
bool randomEventOccurred = sample < luck;

Distributions supported by both Troschuetz.Random and StatDist

Here’s the functions you can use. Also check out this article by the package author and the API docs.

double Beta(double alpha, double beta);

0 < α < ∞
0 < β < ∞
0 ≤ X ≤ 1
View on StatDist
View on Wikipedia

int Binomial(double alpha /* trials */, int beta /* probability */);

0 ≤ α ≤ 1
β ∈ { 0, 1, … }
X ∈ { 0, 1, …, β }
View on StatDist
View on Wikipedia

double Cauchy(double alpha /* location */, double gamma /* scale */);

-∞ < α < ∞
0 < γ < ∞
-∞ < X < ∞
View on StatDist
View on Wikipedia

double ChiSquare(int alpha /* degrees of freedom */);

α ∈ { 1, 2, … }
0 ≤ X < ∞
View on StatDist
View on Wikipedia

double ContinuousUniform(double alpha /* min */, double beta /* max */);

α ≤ β < ∞
-∞ < α ≤ β
α ≤ X < β
View on StatDist
View on Wikipedia

int DiscreteUniform(int alpha /* min */, int beta /* min */);

α ∈ { …, β-1, β}
β ∈ { α, α+1, … }
X ∈ { α, α+1, …, β-1, β }
Not on StatDist, but see the continuous version above
View on Wikipedia

double Erlang(int alpha /* shape */, double lambda /* rate */);

0 < α < ∞
λ ∈ { 1, 2, … }
0 ≤ X < ∞
View on StatDist
View on Wikipedia

double Exponential(double lambda /* rate */);

0 < λ < ∞
0 ≤ X < ∞
View on StatDist
View on Wikipedia

double FisherSnedecor(int alpha, int beta);

α ∈ {1, 2, … }
β ∈ {1, 2, … }
0 ≤ X < ∞
View on StatDist
View on Wikipedia

double Gamma(double alpha /* shape */, double beta /* scale */);

0 < α < ∞
0 < β < ∞
0 ≤ X < ∞
View on StatDist
View on Wikipedia

double Laplace(double alpha /* location */, double mu /* scale */);

0 < α < ∞
-∞ < μ < ∞
-∞ < X < ∞
View on StatDist
View on Wikipedia

double Logistic(double mu /* mean */, double sigma /* scale */);

-∞ < μ < ∞
0 < σ < ∞
-∞ < X < ∞
View on StatDist
View on Wikipedia

double Lognormal(double mu /* mean */, double sigma /* standard deviation */);

-∞ < μ < ∞
0 ≤ σ < ∞
0 ≤ X < ∞
View on StatDist
View on Wikipedia

double Normal(double mu /* mean */, double sigma /* standard deviation */);

-∞ < μ < ∞
0 < σ < ∞
-∞ < X < ∞
View on StatDist
View on Wikipedia

double Pareto(double alpha /* scale */, double beta /* shape */);

0 < α < ∞
0 < β < ∞
α ≤ X < ∞
View on StatDist
View on Wikipedia

int Poisson(double lambda /* rate */);

0 < λ < ∞
X ∈ { 0, 1, … }
View on StatDist
View on Wikipedia

double Rayleigh(double sigma /* scale */);

0 < σ < ∞
0 ≤ X < ∞
View on StatDist
View on Wikipedia

double StudentsT(int nu /* degrees of freedom */);

ν ∈ { 1, 2, … }
-∞ < X < ∞
View on StatDist
View on Wikipedia

double Triangular(double alpha /* min */, double beta /* mode */, double gamma /* max */);

-∞ < α < β
α < β < ∞
α ≤ γ ≤ β
α ≤ X ≤ β
View on StatDist
View on Wikipedia

double Weibull(double alpha /* shape */, double lambda /* scale */);

0 < α < ∞
0 < λ < ∞
0 ≤ X < ∞
View on StatDist
View on Wikipedia